Answer:
Approximately
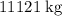 (rounded to the nearest whole number as required, assuming that planet Earth is a uniform sphere.)
(rounded to the nearest whole number as required, assuming that planet Earth is a uniform sphere.)
Step-by-step explanation:
Let
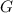 denote the gravitational constant.
denote the gravitational constant.
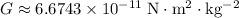 .
.
Let
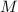 denote the mass of planet Earth. Let
denote the mass of planet Earth. Let
 denote the mass of the telescope. Let
denote the mass of the telescope. Let
 denote the distance between the telescope and the center of planet Earth.
denote the distance between the telescope and the center of planet Earth.
Note the unit conversion for the distance
 :
:
 .
.
By Newton's Law of Universal Gravitation, the magnitude of the gravitational force between planet Earth and this telescope would be:
 .
.
Rearrange this equation to find the mass
 telescope in terms of
telescope in terms of
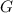 ,
,
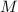 , and
, and
 :
:
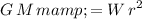 .
.
 .
.
Substitute in the value of
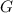 ,
,
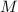 , and
, and
 :
:
 .
.