Question

Solve for the value of v.

Answer 1

9

Explanation:

Since it is a straight line, therefore it will always be 180°

So...

(8v +3) +105 = 180

8v + 3 + 105 = 180

8v = 180 - 108

V = 72/8

= 9

Answer 2

`\boxed {\boxed {\sf v=9}}`

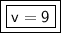
Explanation:

In the diagram, there are 2 angles: 105° and (8v+3)°. They are on a straight line together, so they are supplementary angles. They must add to 180 degrees. We can set up an equation.

`105 + (8v+3) = 180`

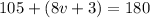
We are solving for v, so we must isolate the variable. First, we can rearrange the right side and combine the like terms (the constants without a variable).

`105 +8v+3= 180 \\8v + (105+3) = 180 \\8v + 108= 180`

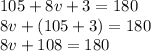
108 is being added to 8v. The inverse operation of addition is subtraction. Subtract 108 from both sides of the equation.

`8v+108-108= 180-108 \\8v= 180-108 \\8v=72`

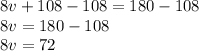
v is being multiplied by 8. The inverse operation of multiplication is division. Divide both sides by 8.

`\frac {8v}{8}= (72)/(8)\\`

`v= (72)/(8)`

`v=9`

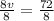
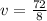
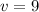
v is equal to 9.