Answer:
7
Explanation:
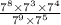
Step 1 : simplify denominator and numerator.
To do this we must multiply the numbers on top as well as the numbers on the bottom.
Multiplying exponents with the same base rule:
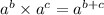
so when multiplying exponents with the same base we simply keep the base the same and add the exponents
using this rule we can simplify the denominator and numerator
Denominator :
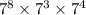
keep the base the same and add the exponents
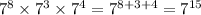
Numerator:
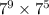
keep the base the same and add the exponents
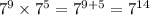
We now have
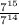
Next we must divide the exponents.
Dividing exponent rule ( with same base )
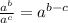
So when dividing exponents with the same base we simply keep the base the same and subtract the exponent of the denominator by the exponent of the numerator
Applying this we get
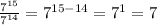
And we are done!