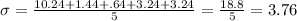Answer:
Explanation:
To find the population variance, we first need the mean:
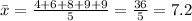 so the mean is 7.2. To find the population variance (which is almost exactly the same as the sample variance except for a small difference in the denominators of the formula) we have to take each number minus the mean, and then square the difference. Add together all these squared numbers and then divide by the number of numbers. Like this:
so the mean is 7.2. To find the population variance (which is almost exactly the same as the sample variance except for a small difference in the denominators of the formula) we have to take each number minus the mean, and then square the difference. Add together all these squared numbers and then divide by the number of numbers. Like this:
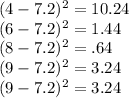
Add together those numbers and divide them by 5: