Answer:
Beach to parking lot = 24 m
Parking lot to refreshment stand = 40 m
Explanation:
Part a
Right triangle altitude theorem:
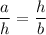
This theorem describes the relationship between the altitude (h) on the hypotenuse in a right triangle and the two line segments (a and b) it creates on the hypotenuse. (a is the shorter segment and b is the longer segment of the hypotenuse).
For the given triangle:
- h = the distance between the parking lot and the beach
- a = 18 m
- b = 32 m
Substituting these values into the formula:
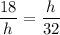
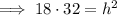


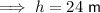
So the distance between the beach and the parking lot is 24 m
Part b
We can now use Pythagoras' Theorem to calculate the distance between the parking lot and the refreshment stand.
Pythagoras' Theorem: a² + b² = c²
(where a and b are the legs, and c is the hypotenuse, of a right triangle)
Given:
- a = 24
- b = 32
- c = distance between refreshment stand and parking lot
Substituting these values into the formula:
⇒ 24² + 32² = c²
⇒ c² = 1600
⇒ c = √1600
⇒ c = 40 m
Therefore, the distance between the parking lot and the refreshment stand is 40 m.