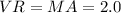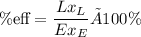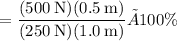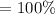Question

Please tell me answer please otherwise teacher will beat me fast ​

Answer 1

Step-by-step explanation:

a) Use the torque equation to solve for the amount of effort to lift the load:

`\sum{\tau} = Lx_L - Ex_E = 0`

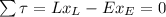
or

`E = (Lx_L)/(x_E) = \frac{(100\:\text{N})(0.20\:\text{m})}{0.60\:\text{m}}`

`\:\:\:\:\:=33.3\:\text{N}`

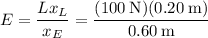
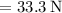
The mechanical advantage is

`MA = \frac{0.60\:\text{m}}{0.20\:\text{m}} = 3`

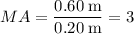
The velocity ratio is the same as the MA:

`VR = \frac{\text{effort arm}}{\text{load arm}} = MA = 3`

b) We can use the same equation in (a) to solve the problem:

`\sum{\tau} = Ex_E - Lx_L = 0`

`\Rightarrow x_L = (Ex_E)/(L) = \frac{(50\:\text {N})(90\:\text{cm})}{300\:\text{N}}`

`\:\:\:\:\:=15\:\text{cm}`

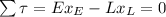
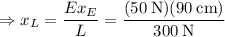
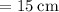
c) We can write

`W_RX_R = W_SX_S \Rightarrow X_R = (W_SX_S)/(W_R)`

`\:\:\:\:\:= \frac{(400\:\text{N})(4\:\text{m})}{500\:\text{N}} = 3.2\:\text{m}`

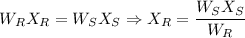
d) We can solve the problem as follows:

`\sum{\tau} = Ex_E - Lx_L = 0 \Rightarrow E = (Lx_L)/(x_E)`

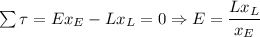
or

`E = \frac{(500\:\text{N})(0.50\:\text{m}}{1.0\:\text{m}} =250\:\text{N}`

The mechanical advantage MA is

`MA = (x_E)/(x_L) = \frac{1.0\:\text{m}}{0.5\:\text{m}} = 2.0`

`VR = MA = 2.0`

`\%\text{eff} = (Lx_L)/(Ex_E)×100\%`

`\:\:\:\:\:= \frac{(500\:\text{N})(0.5\:\text{m})}{(250\:\text{N})(1.0\:\text{m})}×100\%`

`\:\:\:\:\:=100\%`