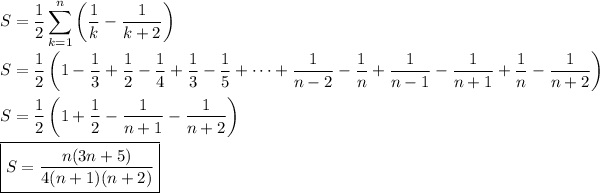Question

Find the sum S:


`\displaystyle \large{S = (1)/(1 \cdot 3) + (1)/(2 \cdot 4) + (1)/(3 \cdot 5) + .... + (1)/(n(n+2))}`
Please show your work too. Thank you!​

Answer 1

Write the sum as

`\displaystyle S = \sum_(k=1)^n \frac1{k(k+2)}`

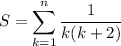
Decompose the summand into partial fractions; that is, we look for constants a and b such that

`\frac 1{k(k+2)} = \frac ak + \frac b{k+2}`

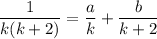
Condense the right side into a single fraction and set the numerators on both sides equal to one another:

`\frac1{k(k+2)} = (a(k+2))/(k(k+2)) + (bk)/(k(k+2)) = (a(k+2)+bk)/(k(k+2)) \\\\ \implies 1 = a(k+2) + bk = (a+b)k + 2a`

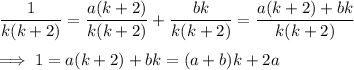
Then a + b = 0 and 2a = 1, so it follows that a = 1/2 and b = -1/2.

We then see that S is a telescoping sum (intermediate terms cancel and the overall sum collapses into a small number of terms):

`\displaystyle S = \frac12 \sum_(k=1)^n \left(\frac1k - \frac1{k+2}\right) \\\\ S = \frac12 \left(1-\frac13 + \frac12 - \frac14 + \frac13 - \frac15 + \cdots + \frac1{n-2} - \frac1n + \frac1{n-1} - \frac1{n+1} + \frac1n - \frac1{n+2}\right) \\\\ S = \frac12 \left(1 + \frac12 - \frac1{n+1} - \frac1{n+2}\right) \\\\ \boxed{S = (n(3n+5))/(4(n+1)(n+2))}`