Question

Find the sum S below:


`\displaystyle \large{S = (2)/(1 \cdot 3) + (2)/(3 \cdot 5) + (2)/(5 \cdot 7) + ... + (2)/((2n - 1)(2n + 1)) }`
Please show your work too. Thanks!​

Answer 1

You can use the same technique I showed in another one of your questions (24467305).

Partial fractions:

`\frac2{(2n-1)(2n+1)} = \frac a{2n-1} + \frac b{2n+1} \\\\ \implies 2 = a(2n+1) + b(2n-1) = (2a+2b)n + a- b \\\\ \implies \begin{cases}2a+2b=0 \\ a-b = 2\end{cases} \implies a = 1, b=-1`

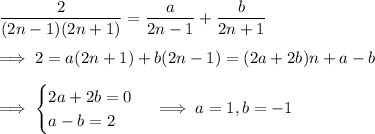
Then we have a telescoping sum,

`S = \displaystyle \sum_(k=1)^n \frac 2{(2k-1)(2k+1)} \\\\ S = \sum_(k=1)^n \left(\frac1{2k-1} - \frac1{2k+1}\right) \\\\ S = 1-\frac13 + \frac13 - \frac15 + \cdots +\frac1{2n-3}-\frac1{2n-1}+\frac1{2n-1}-\frac1{2n+1} \\\\ S = 1 - \frac1{2n+1} = \boxed{(2n)/(2n+1)}`

(And in case you were actually interested in an infinite sum, we can see that this converges to 1 as n goes to ∞.)