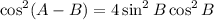Question

Could someone please assist me​

Answer 1

See Below.

Explanation:

We are given that:

`\displaystyle \cos(A - B) = \cos A\cos B + \sin A \sin B`

Part 5.2.1

Note that:

`\displaystyle \cos ( A + B) = \cos (A - (-B))`

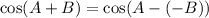
Then from the given identity:

`\displaystyle \cos(A - (-B)) = \cos A \cos( -B) + \sin A \sin (-B)`

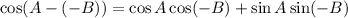
Cosine is an even function and sine is an odd function. That is:

`\displaystyle \cos(- \theta) = \cos \theta \text{ and } \sin (-\theta) = -\sin\theta`

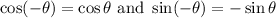
Hence:

`\displaystyle \cos(A + B) = \cos A \cos B - \sin A \sin B`

Part 5.2.2

We want to verify that:

`\displaystyle \cos^2 (A - B) = 4\cos^2 B \sin^2 B`

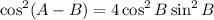
From the identity:

`\displaystyle \cos (A - B) = \cos A \cos B + \sin A \sin B`

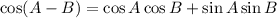
Since A + B = 90°, A = 90° - B. Hence:

`\displaystyle \cos (A - B) = \cos (90^\circ - B) \cos B + \sin (90^\circ - B) \sin B`

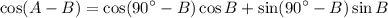
Sine and cosine are co-functions. That is:

`\displaystyle \sin \theta = \cos (90^\circ - \theta) \text{ and } \cos\theta = \sin(90^\circ - \theta)`

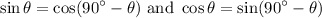
Hence:

`\displaystyle \cos (A - B) = \sin B\cos B + \sin B \cos B = 2\sin B \cos B`

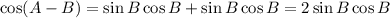
And by squaring both sides:

`\displaystyle \cos ^2 (A - B) = 4\sin^2 B\cos^2 B`