Answer:
Part 5.1.1:
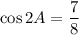
Part 5.1.2:

Explanation:
We are given that:

Part 5.1.1
Recall that:
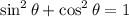
Let θ = 2A. Hence:

Square the original equation:
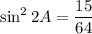
Hence:
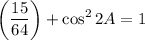
Subtract:
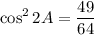
Take the square root of both sides:
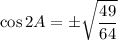
Since 0° ≤ 2A ≤ 90°, cos(2A) must be positive. Hence:
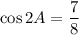
Part 5.1.2
Recall that:
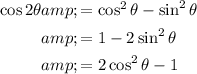
We can use the third form. Substitute:
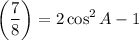
Solve for cosine:
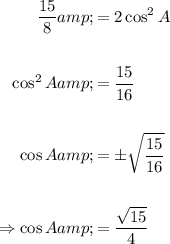
In conclusion:

(Note that since 0° ≤ 2A ≤ 90°, 0° ≤ A ≤ 45°. Hence, cos(A) must be positive.)