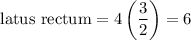Question

Find the vertex and length of the latus rectum for the parabola. y=1/6(x-8)^2+6

Answer 1

Explanation:

If the parabola has the form

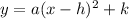`y = a(x - h)^2 + k` (vertex form)

then its vertex is located at the point (h, k). Therefore, the vertex of the parabola

`y = (1)/(6)(x - 8)^2 + 6`

is located at the point (8, 6).

To find the length of the parabola's latus rectum, we need to find its focal length f. Luckily, since our equation is in vertex form, we can easily find from the focus (or focal point) coordinate, which is

`\text{focus} = (h, k +(1)/(4a))`

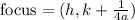
where
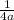`(1)/(4a)` is called the focal length or distance of the focus from the vertex. So from our equation, we can see that the focal length f is

`f = (1)/(4((1)/(6))) = (3)/(2)`

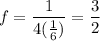
By definition, the length of the latus rectum is four times the focal length so therefore, its value is

`\text{latus rectum} = 4\left((3)/(2)\right) = 6`