Answer:
D(-2, 5).
Explanation:
We are given that M is the midpoint of CD and that C = (10, -5) and M = (4, 0).
And we want to determine the coordinates of D.
Recall that the midpoint is given by:
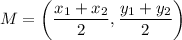
Let C(10, -5) be (x₁, y₁) and Point D be (x₂, y₂). The midpoint M is (4, 0). Hence:
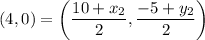
This yields two equations:
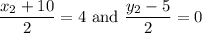
Solve for each:
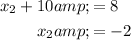
And:

In conclusion, Point D = (-2, 5).