Answer:
The distance between F and A is approximately 6.71 units.
Explanation:
To find the distance between any two points, we can consider using the distance formula. Recall that:
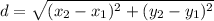
Let F(-2, 1) be (x₁, y₁) and A(4, -2) be (x₂, y₂).
Substitute and evaluate:
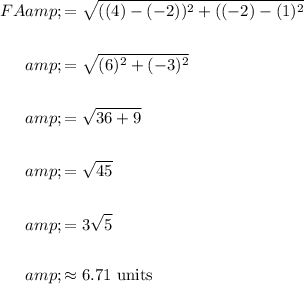
In conclusion, the distance between F and A is approximately 6.71 units.