Explanation:
So let classify each function.
38 is a quadratic because it has a leading variable raised to the 2nd degree.
Quadratics always accept all x values positive or negative so the domain
- All Real Numbers, (- ♾,♾)
Quadratics lowest range is it vertex. The vertex of a typically quadratic is 0 because when we have the function
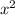
we have no value after it so 0 is the lowest number.
However we have
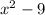
So this means that our lowest value will be -9.
We include that point as well. The leading coeffceint is positive so it approach infinity so the range is
39 is a square root function because it has the square root symbol. Remeber that we can't take the square root of a negative number i.e( we can but it isn't graphable on a Cartesian plane). So this means x has to be greater than or equal to zero. We can take the square root of 0.
So set the equation inside the radical equal to zero.
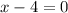
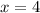
So this means the domain is
In a square root function, we restrict our domain to only positive number so the range is
[0,♾)