Answer:
The water level would rise by
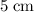 .
.
Explanation:
Assume that the initial water level is
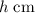 .
.
Before the cube was placed in the tank, the volume of the water was the same as the volume of a rectangular prism with a length of
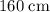 , a height of
, a height of
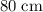 , and a height of
, and a height of
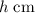 :
:
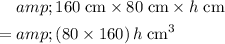 .
.
Let the rise in the water level in the tank be
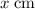 . The new water level would be
. The new water level would be
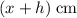 .
.
The volume of the water and the submerged cube, combined, would be the same as that of a rectangular prism with a length of
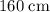 , a width of
, a width of
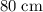 , and a height of
, and a height of
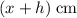 :
:
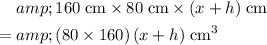 .
.
In other words:
- Volume of water in this tank:
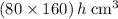 , whereas
, whereas - Volume of water in this tank, plus the volume of the submerged cube:
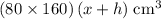 .
.
Therefore, the volume of the submerged cube could be expressed as:
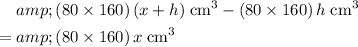 .
.
On the other hand, the volume of the cube could be expressed as:
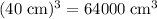 .
.
Equate these two expressions for the volume of the cube and solve for
 , the rise in the water level in the tank:
, the rise in the water level in the tank:
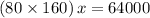 .
.
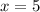 .
.
In other words, the rise in the water level in this tank would be
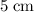 .
.