Question

Find the distance between the two points rounding to the nearest tenth (4,0) and (0,9)

Answer 1

`\boxed {\boxed {\sf 9.8}}`

Explanation:

We are asked to find the distance between two points. We will calculate the distance using the following formula;

`d= \sqrt {(x_2-x_1)^2+(y_2-y_1)^2`

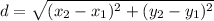
In this formula, (x₁ , y₁) and (x₂ , y₂) are the 2 points. We are given the points (4,0) and (0,9). If we match the value and the corresponding variable, we see that:

• x₁= 4
• y₁= 0
• x₂= 0
• y₂= 9

Substitute the values into the formula.

`{d= \sqrt {(0-4)^2+(9-0)^2`

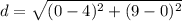
Solve inside the parentheses.

• (0-4)= -4
• (9-0)= 9

`d=\sqrt{(-4)^2+ (9)^2`

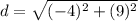
Solve the exponents. Remember that squaring a number is the same as multiplying it by itself.

• (-4)²= -4*-4= 16
• (9)²= 9*9= 81

`d= \sqrt{(16)+(81)`

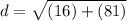
Add.

`d= \sqrt{97`

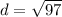
Take the square root of the number.

`d=9.848857802`

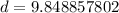
Round to the nearest tenth. The 4 in the hundredth place tells us to leave the 8 in the tenth place.

`d\approx 9.8`

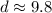
The distance between the two points (4,0) and (0,9) is approximately 9.8