Since log(ab) = log(a) + log(b) and log(a/b) = log(a) - log(b) for any logarithm base, we have
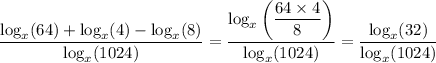
Then using the change-of-base identity, we have
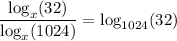
But we also know that 2¹⁰ = 1024 and 2⁵ = 32, so we can back up slightly and instead write
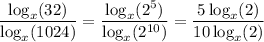
Then the logarithms cancel and you're left with 5/10 = 1/2.