Question

Plz help answer this question

Answer 1

Option I

Explanation:

Let

`f(x)=x^2+3x-28`

We know by subsitution,

`f(-9)=(-9)^2+3(-9)-28=26>0`

`f(0)=0^2+3(0)-28=-28<0`

`f(5)=5^2+3(5)-28=12>0`

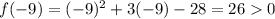
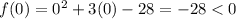
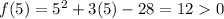
Since a quadratic equation only have 1 turning point, we know for some values a in (-9, 5) such that f(a)<0. And the option of the range of a must lie with in (-9, 5).

Therefore, only Option I is correct.