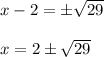Question

Please show all steps and explain what you did thoroughly, thank you for your time and help.

1. Solve by using the quadratic formula: x^2 + 6x + 11 = 0
2. Solve by completing the square: 2x^2 - 16x = 50

Answer 1

Explanation:

1) x² + 6x + 11 = 0

a = coefficient of x² = 1

b = coefficient of x = 6

c = Constant = 11

Roots = (-b ± √b² - 4ac)/2a

`D = \sqrt{b^(2)-4ac}\\\\=\sqrt{6^(2)-4*1*11}\\\\=√(36-44)\\\\=√(-8)\\\\=\sqrt{8i^(2)}\\\\ = 2i√(2)`

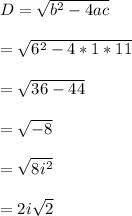
Roots =
`(-6 \± 2i√(2))/(2)\\`

`= (2(-3 \± i√(2)))/(2)\\\\=-3 \± i√(2)`

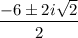
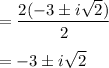
2) 2x² - 16x = 50

Divide the whole equation by 2

x² - 8x = 25

Divide the coefficient of x (i. e 8 ) by 2 = 8/2 = 4, Now add 4 to both sides of the equation

x² - 8x + 4 = 25 + 4

x² - 2*4*x + 2² = 29

(x - 2)² = 29

Take square root both side

`x - 2 = \± √(29)\\\\x = 2 \± √(29)`