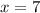Question

X =sqrt(x+18)+2

explain please

Answer 1

Let's find x

`\\ \rm\rightarrowtail x=√(x+18)+2`

`\\ \rm\rightarrowtail x-2=√(x+18)`

`\\ \rm\rightarrowtail x^2-4x+4={x+18}`

`\\ \rm\rightarrowtail x^2-5x-14=0`

`\\ \rm\rightarrowtail x^2+2x-7x-14=0`

`\\ \rm\rightarrowtail (x+2)(x-7)=0`

• x=-2,7

Answer 2

`x=7`

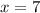
Explanation:

`x =√((x+18))+2`

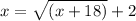
subtract 2 from both sides:

`x -2=√((x+18))`

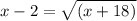
square both sides:

`(x -2)^2=x+18`

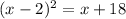
expand brackets:

`x^2-4x+4=x+18`

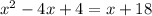
subtract x from both sides:

`x^2-5x+4=18`

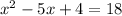
subtract 18 from both sides:

`x^2-5x-14=0`

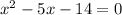
factor:

`x^2+2x-7x-14=0`

`x(x+2)-7(x+2)=0`

`(x+2)(x-7)=0`

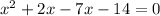
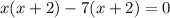
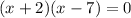
solve for x:

`x+2=0\implies x=-2`

`x-7=0\implies x=7`

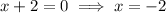
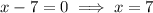
Now we have found the values of x, input them into the original equation to verify:

when
`x = -2`:

`√((-2 +18))+2=6\\\\ 6\\eq 2\implies \textsf {incorrect}`

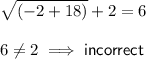
when
`x = 7`:

`√((7+18))+2=7\\\\ 7=7\implies \textsf {correct}`

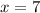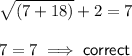
Therefore, the only correct solution is
`x=7`