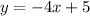Answer:
Explanation:
We want to find the equation of the line that is perpendicular to:

And which passes through the point (2, -3).
Recall that the slopes of perpendicular lines are negative reciprocals of each other.
In other words, since the slope of the original line is 1/4, the slope of the perpendicular line will be -4.
We are also given that it passes through the point (2, -3). Hence, we can consider using the point-slope form:

Substitute:
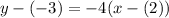
Simplify:
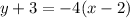
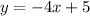
Distribute:
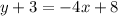
And subtract:
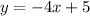
In conclusion, our equation is: