Answer:
PQ measures 36 units.
Explanation:
Line RS bisects segment PQ at R. By the definition of a bisector:
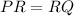
Hence:
We are given that RQ = x + 9 and RP = 2x, and we want to determine PQ.
Solve for x. Substitute:
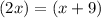
Hence:
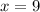
PQ is given by:
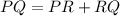
Since PR = RQ:
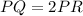
Substitute and evaluate:
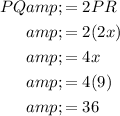
Hence, PQ measures 36 units.