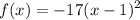Question

write a quadratic function in vertex form whose graph has the vertex (1,0) and passes through point (2,-17)

Answer 1

`\displaystyle f(x) = -17(x-1)^2`

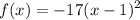
Explanation:

We want to write a quadratic function in vertex form whose vertex is (1, 0) and passes through the point (2, -17).

Recall that vertex form is given by:

`\displaystyle f(x) = a(x-h)^2 + k`

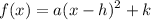
Where (h, k) is the vertex and a is the leading coefficient.

Since our vertex is at (1, 0), h = 1 and k = 0:

`\displaystyle f(x) = a(x-1)^2`

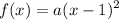
It passes through the point (2, -17). Hence, when x = 2, y = -17:

`\displaystyle (-17) = a((2)-1)^2`

Solve for a:

`\displaystyle a = -17`

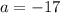
In conclusion, our quadratic function in vertex form is:

`\displaystyle f(x) = -17(x-1)^2`