Answer:
The ball is six feet above the ground after two seconds.
Explanation:
The height of a projectile as a function of time is modeled by the function:

And we want to determine after how many seconds is the ball six feet above the ground.
In other words, we can let h(t) = 6 and solve for t. This yields:
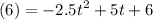
Solve for t:

By the Zero Product Property:
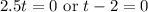
Hence:

In conclusion, the ball is six feet above the ground after two seconds.