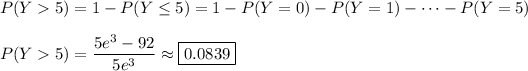Given the PMF
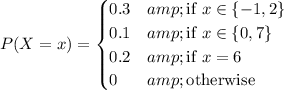
(a)
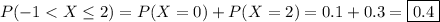
(b) The CDF is defined as
 , so that
, so that

It follows that
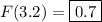
(c) Expectation is defined as
![E[X] = \displaystyle \sum_x x\,P(X=x)](https://img.qammunity.org/2022/formulas/mathematics/college/xd8sko6tzgq3jz35aqbvmmnvb4210ay8rb.png)
We have
![E[X] = \displaystyle \sum_{x\in\{-1,0,2,6,7\}} x\,P(X=x) \\\\ E[X] = -P(X=-1) + 2P(X=2)+6P(X=6)+7P(X=7) \\\\ E[X] = -0.3 + 0.6 + 1.2 + 0.7 = \boxed{2.2}](https://img.qammunity.org/2022/formulas/mathematics/college/kxsn2w7sx8pz7isjoqj3pcglr2aib8mqx5.png)
(d) First compute the second moment of X, which is defined as
![E[X^2] = \displaystyle \sum_x x^2\,P(X=x)](https://img.qammunity.org/2022/formulas/mathematics/college/7d455bn8nwumitoduz02z83vsehhl2ubax.png)
We get
![E[X^2] = (-1)^2P(X=-1) + 2^2P(X=2) + 6^2P(X=6) + 7^2P(X=7) \\\\ E[X^2] = 0.3 + 1.2 + 7.2 + 4.9 = 13.6](https://img.qammunity.org/2022/formulas/mathematics/college/8smn8rv9m2rn0gzif8hvei48wblj50z18k.png)
Variance is defined as
![\mathrm{Var}[X] = E[(X - E[X])^2] = E[X^2] - E[X]^2](https://img.qammunity.org/2022/formulas/mathematics/college/nolovgf0h1hawd6kv1s5h6gyacoeswoohp.png)
so it follows that
![\mathrm{Var}[X] = 13.6 - 2.2^2 = \boxed{8.76}](https://img.qammunity.org/2022/formulas/mathematics/college/f186lshnmw4va0b8x49oen2eisne7ro01y.png)
(e) Not sure what this part has to do with the rest of the question. At any rate, if Y is a random variable following a Poisson distribution with λ = 3, then Y has a PDF of
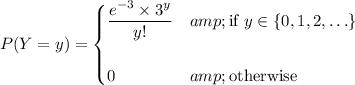
Then