Question

Mario plays a game that involves drawing cards to move around the board. He uses a uniform probability model to determine the

probability that he will win on his next turn. There are 6 red cards, 6 yellow cards, 6 orange cards, 6 purple cards, 6 blue cards, 6
green cards, and 6 black cards. Mario needs either a purple or a green card to win on his next turn.
What is P (purple or green)?
o
ده
15
ob
ОО
이을
So I
0 1 / 3

Answer 1

Given :

• 6 red cards
• 6 yellow cards
• 6 orange cards
• 6 purple cards
• 6 blue cards
• 6 green cards
• 6 black cards

To find:

The probability that the chosen card is either purple or green

Solution:

Total number of cards ⇢42 cards

• 6 red cards+6 yellow cards+ 6 orange cards+ 6 purple cards+ 6 blue cards+ 6 green cards + 6 black cards

Total number of required card ⇢ 12 cards

• 6 purple cards + 6 green cards ⇢12 cards

probability of getting a purple or green card↷

`⇢probability = \frac{favourable \: outcomes} {possible \: outcomes}\\`

`⇢ (12)/(42) \\`

`⇢ (2)/(7) \\`

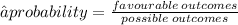
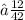
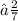
Hence , option 3 ⇢ 2/7 is correct ✓

Answer 2

2/7

Explanation:

There are 6 each of 7 different colored cards.

Therefore, total number of cards = 7 × 6 = 42

So the probability of each color card being chosen = 6/42 = 1/7

⇒ P(purple) = 1/7

⇒ P(green) = 1/7

So P(purple or green) = P(purple) + P(green)

= 1/7 + 1/7

= 2/7