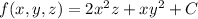Question

For the following vector fields, find its curl and determine if it is a gradient field.

F= (4xz+ y^2) i + 2xyj+ 2x^2k

Answer 1

Given

`\vec F = (4xz+y^2)\,\vec\imath + 2xy\,\vec\jmath + 2x^2\,\vec k`

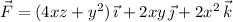
its curl would be

`\\abla*\vec F = \left((\partial(2xy))/(\partial z) - (\partial(2x^2))/(\partial y)\right)\,\vec\imath - \left((\partial(4xz+y^2))/(\partial z) - (\partial(2x^2))/(\partial x)\right)\,\vec\jmath + \left((\partial(4xz+y^2))/(\partial y) - (\partial(2xy))/(\partial x)\right)\,\vec k`

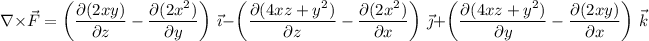
which reduces to the zero vector. Since the curl is zero, and
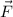`\vec F` doesn't have any singularities,
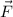`\vec F` is indeed a gradient field.

To determine what it is a gradient of, we look for a scalar function f(x, y, z) such that
`\\abla f = \vec F`. This entails solving for f such that

`(\partial f)/(\partial x) = 4xz+y^2 \\\\ (\partial f)/(\partial y) = 2xy \\\\ (\partial f)/(\partial z) = 2x^2`

Integrate both sides of the first equation with respect to x, which gives

`f(x,y,z) = 2x^2z+xy^2 + g(y,z)`

Differentiate both sides of this with respect to y :

`(\partial f)/(\partial y) = 2xy = 2xy+(\partial g)/(\partial y) \\\\ \implies (\partial g)/(\partial y) = 0 \implies g(y,z) = h(z)`

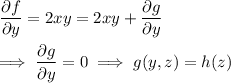
Differentiate f with respect to z :

`(\partial f)/(\partial z) = 2x^2 = 2x^2 + (\mathrm dh)/(\mathrm dz) \\\\ \implies (\mathrm dh)/(\mathrm dz) = 0\implies h(z) = C`

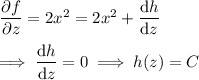
So it turns out that
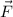`\vec F` is the gradient of

`f(x,y,z) = 2x^2z+xy^2+C`