Question

99. Savings Bronwyn wants to buy a house, so she has decided

to save one quarter of her salary. Bronwyn earns $47.00 per hour
and receives an extra $28.00 a week because she declined
company benefits. She wants to save at least $550.00 each week.
How many hours must she work each week to achieve her goal?

Answer 1

46.5 hours per week

Explanation:

At least 550 a week.

Which is 1\4 of Bronwyn salary.

550 x 4 = 2200

To find minimum work hours

2200-28 = 2172

2172 \ 47 = 46.212 hours per week

So, bronwyn needs to work at least 46.5 hours per week

Answer 2

Bronwyn must work nearly 47 hours each week to achieve her goal.

Explanation:

Let x be the number of hours Bronwyn works per week.

If Bronwyn earns $47 per hour, if x is the number of hours she works per week and if Bronwyn earns $28 per week because she declined company benefits, lets assume that the left hand side of the equation is:

`47x + 28`

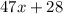
Now onto the salary. Since Bronwyn wants to save $550 each week and since she also wants to save one quarter of her salary, her salary becomes $2200 for each week she works

Making the equation...

`47x + 28 = 2200`

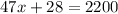
Time to solve for x

`47x = -28 + 2200\\47x = 2172\\x = 46.2`

Since its at least, you can round it up to 47 making 47 the number of hours she must work each week to achieve her goal.