Answer:
The gas particles would have higher Kinetic energy.
Step-by-step explanation:
From the formular of kinetic energy:

KE is the kinetic energy possessed by particle.
KE is the kinetic energy possessed by particle.m is the particle mass.
KE is the kinetic energy possessed by particle.m is the particle mass.v is the velocity attained by a particle
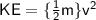
keeping the mass, m constant:

Therefore, KE is directly proportional to v² :

so, when velocity increases, KE also increases.