Answer:
7.2 cm
Explanation:
The adjacent interior angles of a rhombus must be supplementary.
Let ABCD be the rhombus whose area is 40 cm².
Let the diagonals AC and BD intersect at O.
If s is the side, one-half diagonal = s× sin(25) and the other is s× sin(65) = s × cos(25)
Area of a rhombus = ½× (a×b)²× sin(ø)]
side length, a = b
Area of rhombus = ½× s² × sin(25)cos(25)
40 cm² = ½ × s² × sin(25)cos(25)
sin(a)cos(b) = 2[sin(x+y)+sin(x-y)]
sin(a)cos(b) = 2[sin(x+y)+sin(x-y)] Since x = y = 25°
sin(a)cos(b) = 2[sin(x+y)+sin(x-y)] Since x = y = 25°sin(a)cos(b) = 2[sin(x+y)]
》40 cm² = ½ × s² × 2sin(50)
》40 cm² = s² × sin(50)
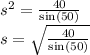
s = 7.2260841106 cm
Therefore, the length of the side of a rhombus, s is 7.2 cm