Step-by-step explanation:
You have already determined the components of the known forces so I won't repeat your work here. Since the resultant force
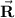 and F1 are completely along the x-axis, we can conclude that
and F1 are completely along the x-axis, we can conclude that
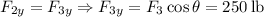
We can now solve for the magnitude of
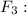
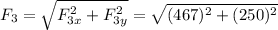

The angle
 is then
is then

or
