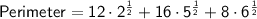Answer:
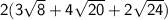
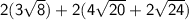
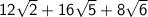
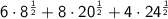
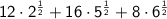
Explanation:
Perimeter of a rectangle
Perimeter = 2(width + length)
Given information:
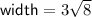
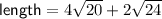
Equivalent Expression 1
Substitute the given information into the formula:
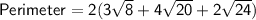
Equivalent Expression 2
Using the distributive property law, this can also be written as:
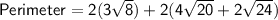
Equivalent Expression 3
Distribute the parentheses and simplify the radicals:
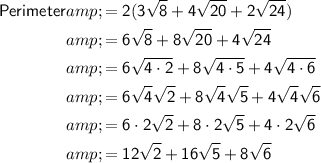
Equivalent Expression 4
Distribute the parentheses and rewrite the square roots as
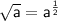 :
:
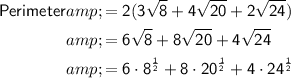
Equivalent Expression 5
Rewrite the square roots as
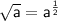 :
: