Question

Two question here please answer it correctly

40. Evaluate f (x2-2xy)dx +(x2y+3)dy around the boundary of the region defined by y2 = 8x and x = 2
(a) directly, (b) by using Green's theorem. Ans. 128/5
(TT.2)
41. Evaluate f (6xy - y2) dx + (3x2 --- 2xy) dy along the cycloid x = 6 - sin 6, y = 1 - cos 6.

Answer 1

(40) It looks like the line integral is

`\displaystyle \int_C (x^2-2xy)\,\mathrm dx + (x^2y+3)\,\mathrm dy`

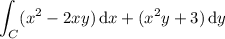
where C is the boundary of the region D,

`D = \left\{(x,y) \mid \frac{y^2}8\le x\le2\text{ and }-4\le y\le4\right\}`

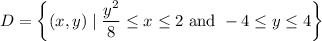
(a) To evaluate the line integral directly, split up C into two paths C₁ and C₂, parameterized by

• C₁ : x = t ²/8 and y = -t, where -4 ≤ t ≤ 4

(the y component is negative to make this path have a positive/counterclockwise orientation)

• C₂ : x = 2 and y = t, where -4 ≤ t ≤ 4

Then the line integral over C is the sum of the line integrals over C₁ and C₂ :

`\displaystyle \int_C = \int_C \left(\left(x(t)^2-2x(t)y(t)\right)(\mathrm dx)/(\mathrm dt) + \left(x(t)^2y(t)-3\right)(\mathrm dy)/(\mathrm dt)\right)\,\mathrm dt \\\\ = \int_(-4)^4 \left(\left(\frac{t^3}4+(t^4)/(64)\right)\frac t4 - \left(3-(t^5)/(64)\right)\right)\,\mathrm dt + \int_(-4)^4 (4t+3)\,\mathrm dt \\\\ = \int_(-4)^4 \left(4t+(t^4)/(16)+(5t^5)/(256)\right)\,\mathrm dt = \boxed{\frac{128}5}`

(b) Using Green's theorem, we have

`\displaystyle \int_C (x^2-2xy)\,\mathrm dx + (x^2+3)\,\mathrm dy = \iint_D (\partial(x^2y+3))/(\partial x) - (\partial(x^2-2xy))/(\partial y)\,\mathrm dx\,\mathrm dy \\\\ = \int_(-4)^4 \int_(y^2/8)^2 (2xy+2x)\,\mathrm dx\,\mathrm dy = \boxed{\frac{128}5}`

# # #

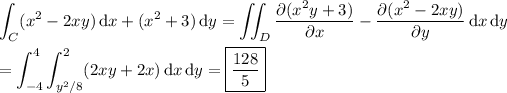
(41) I assume you meant to use θ in the parameterization, and not 6, so that C is parameterized by x = θ - sin(θ) and y = 1 - cos(θ). There's no range given for θ, so I'll just assume 0 ≤ θ ≤ π.

Then ... (for some reason, the math text won't render properly. I've attached the computation as an image)

(where s = sin(θ) and c = cos(θ))