Answer:
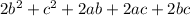
Explanation:
Whenever you have a parentheses to a power of a number you have to make it the parentheses times itself, so (a+b+c)^2 becomes (a+b+c)(a+b+c), where you then multiply a by a, a by b, a by c, b by a, b by b, b by c, and so on and then add all those numbers up. If you do that you would get a^2 + ab + ac + ab + b^2 + bc + ac + bc + c^2, where you then add them up to get a^2 + b^2 + c^2 + 2ab + 2ac + 2bc. Since you have - a^2 after this, you cancel out the a^2, and finally, you have + b^2 so you add b^2 to it and you get a final answer of 2b^2 + c^2 + 2ab + 2ac + 2bc.