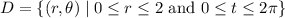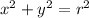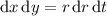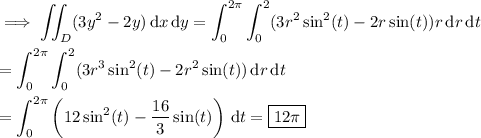Question

Work the previous problem for the line integral f (x2+y2)dx + 3xy2 dy.

Answer 1

Feel free to consult the details in my answer to 24438105 if you wish to compute the line integral directly. I don't see any specification of which method to use, so I'll do it the faster way.

By Green's theorem,

`\displaystyle \int_C (x^2+y^2)\,\mathrm dx + 3xy^2\,\mathrm dy = \iint_D (\partial(3xy^2))/(\partial x) - (\partial(x^2+y^2))/(\partial y)\,\mathrm dx\,\mathrm dy \\\\ = \iint_D (3y^2-2y)\,\mathrm dx\,\mathrm dy`

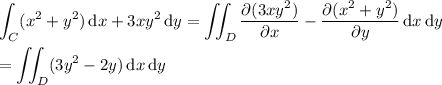
Since D is a disk with radius 2 centered at the origin, consider converting to polar coordinates using x = r cos(t ) and y = r sin(t ). Then

`D = \left\{(r,\theta) \mid 0\le r\le 2\text{ and }0\le t\le2\pi\right\}`

`x^2+y^2 = r^2`

`\mathrm dx\,\mathrm dy = r\,\mathrm dr\,\mathrm dt`

`\implies \displaystyle \iint_D (3y^2-2y) \,\mathrm dx\,\mathrm dy = \int_0^(2\pi)\int_0^2 (3r^2\sin^2(t)-2r\sin(t))r\,\mathrm dr\,\mathrm dt \\\\ = \int_0^(2\pi) \int_0^2 (3r^3\sin^2(t)-2r^2\sin(t))\,\mathrm dr\,\mathrm dt \\\\ = \int_0^(2\pi) \left(12\sin^2(t)-\frac{16}3\sin(t)\right)\,\mathrm dt = \boxed{12\pi}`