Answer:
none
Explanation:
We can start by multiplying both side of the equation by 6 in order to remove the fractions.
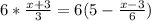

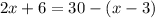
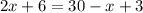
Now, we can try to see if this equation is equivalent to the other options.
Every option has the left side as 2x - 6. In order to get that, we need to subtract 12 on both sides:
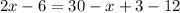
This simplifies to
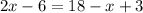
This is not the same as any of the options shown.
We can check this by solving the equations.
2x - 6 = 18 - x + 3
3x = 6 + 18 + 3
3x = 27
x = 9
Now, the first option:
2x - 6 = 10 - x - 3
3x = 6 + 10 - 3
3x = 13
x = 13/3
The second option is the exact same as the third, so they would have the same solution:
2x - 6 = 30 - x- 3
3x = 6 + 30 - 3
3x= 33
x = 11
Since none of the options have the answer 9, they are not equivalent to the equation shown.