Question

A company that makes barber scissors has found that the sales volume for barber scissors is directly proportional to the size of the sales force and inversely proportional to the price of the scissors. If 19440 pairs were sold in 2003, when there were 54 salespeople and the price was $20 a pair, what is the sales forecast for the upcoming year with 50 salespeople and a price of $18 a pair?

Answer 1

20,000 pairs of barber scissors.

Explanation:

The sales volume V for barber scissors is directly proportional to the size S of the sales force and inversely proportional to the price P of the scissors.

In other words, we can write that:

`\displaystyle V = (kS)/(P)`

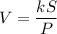
Where k is the constant of proportionality.

19,440 pairs were sold in 2013, when there was 54 salespeople and the price was $20 a pair. Hence, V = 19440 when S = 54 and P = 20. Substitute and determine the value of k:

`\displaystyle \begin{aligned} (19440) &= (k(54))/((20)) \\ \\ 19440 &= (27)/(10)k \\ \\ k &=(10)/(27)(19440) = 7200 \end{aligned}`

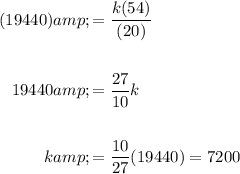
Hence, our equation is:

`\displaystyle V = (7200S)/(P)`

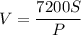
We want to determine the sales forecast with 50 salespeople and a price of $18 a pair. Hence, S = 50 and P = 18:

`\displaystyle \begin{aligned} V&= (7200(50))/((18)) \\ \\ &= 20000\end{aligned}`

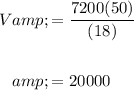
In conclusion, 20,000 pairs of barber scissors can be expected to be sold.