Question

Please help me solve that question​

Answer 1

i). 14/75 or 19%

ii). 2/25 or 8%

Explanation:

i). Using the combinations formula if repetition is allowed

If n choose r,

(r+n-1)!/r!(n-1)!

Where n is the things we have to pick from and r is the objects we want. We want 2 objects and we have 24 objects to pick from.

So our equation will be

(2+24-1)!/2!(24-1)!

(25)!/2!(23)!,

This gives us 300. So there is 300 possible combinations.

Since we have two independent events, we can multiply two events and divide it by 300 to find the probability.

i) There is 14 good defects and 4 major defects so

`(14 * 4)/(300) = (56)/(300) = (14)/(75)`

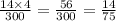
So the probability is 14/75 or 19%

ii) We can do the same thing in question 1

There is 6 minor defects and 4 major so

`(6 * 4)/(300) = (24)/(300) = (8)/(100) = (2)/(25)`

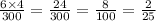
So this means the probability is 8% or 2/25