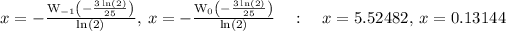Question

5^2x = 3(2^x) find x please show steps

Answer 1

Explanation:

There is a possible issue in your question...

As written it can be interpreted in two ways

like this #1 :

`5^(2x) = 3(2^x)`

or like this #2 :

`5^2x = 3(2^x)`

VERSION #1

divide by the 2^x

`(5^(2x) )/(2^x) = 3`

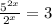
to be able to get to the exponent you have to take "logs"

... look up the rules for logs ... log(ab) = log (a)+log(b) , log(a/b) = log(a)-log(b) etc.

if you take the logs of both sides the using the quotient rule and the exponent rule ....result the result is...

`5^(2x)=3\left(2^x\right)\quad :\quad x=(\ln \left(3\right))/(2\ln \left(5\right)-\ln \left(2\right))\quad \left(\mathrm{Decimal}:\quad x=0.43496\dots \right)`

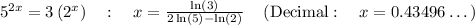
VERSION #2

`5^2x\:=\:3\left(2^x\right)`

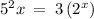
25 x = 3(2^x)

`(25)/(3) = (2^(x) )/(x)`

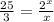
This gets really nasty, and I assume that it is not the original problem..

`x=-\frac{\text{W}_(-1)\left(-(3\ln \left(2\right))/(25)\right)}{\ln \left(2\right)},\:x=-\frac{\text{W}_0\left(-(3\ln \left(2\right))/(25)\right)}{\ln \left(2\right)}\quad \mathrm{ }:\quad x=5.52482 ,\:x=0.13144`

Answer 2

Explanation:

the answer is in the image above