Answer:
centre = (4, -
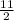 )
)
Explanation:
the equation of a circle in standard form is
(x - h)² + (y - k)² = r²
where (h, k ) are the coordinates of the centre and r is the radius
given
x² + y² - 8x + 11y - 2 = 0 ( collect terms in x and y together and add 2 to both sides )
x² - 8x + y² + 11y = 2
using the method of completing the square
add ( half the coefficient of the x / y terms )² to both sides
x² + 2(- 4)x + 16 + y² + 2(
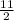 )y +
)y +
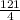 = 2 + 16 +
= 2 + 16 +
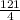
(x - 4)² + (y +
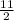 )² =
)² =
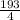 ← in standard form
← in standard form
with centre (4, -
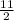 )
)