Question

The sum of the first 20 terms of an arithmetic is 50, and the sum of the next 20 terms is -50. Find the is first term and command difference of the sequence?

​

Answer 1

`a_1=(39)/(8); \ d=-(1)/(4).`

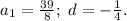
Explanation:

1) if the first term is 'a₁', the difference of the sequence is 'd', then it is possible to write two equations for the sum of the first 20 terms and the next 20 terms;

2) for the first 20 terms: (a₁+a₂₀)*20/2=50;⇔ (a₁+a₁+19d)*10=50; ⇔2a₁+19d=5;

for the next 20 terms: (a₂₁+a₄₀)*20/2= -50;⇔ (a₁+20d+a₁+39d)*10=-50;⇔ 2a₁+59d= -5.

3) if to solve the system of two equations, then:

`\left \{ {{2a_1+19d=5} \atop {2a_1+59d=-5}} \right. \ => \ \left \{ {{a_1=(39)/(8) } \atop {d=-(1)/(4) }} \right.`

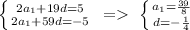
4) finally: the first term is '39/8', the difference is '-1/4'.