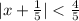Explanation:
First let solve the inequality
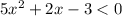
Factor by grouping
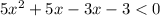

So the factor are
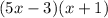
So the factor are
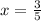
and
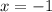
Solutions to a quadratic can be represented by a absolute value equation because remeber quadratics
creates 2 roots and/or double roots.
The inequality
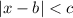
works as
b is the midpoint between 2 roots. And c is the
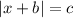
We know that the midpoint between both roots is-1/5.
so

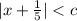
Let use roots 3/5
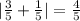
-1 works as well.
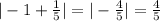
So the absolute value equation is