Answer:
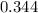
Explanation:
we are given that a coin is tossed 6 times and we want to find the probability of getting at most 2 heads.
To solve this problem,we can consider binomial distribution, which is given by
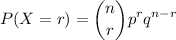
where:
- P = binomial probability
- r = number of times for a specific outcome within n trials
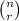 = number of combinations
= number of combinations- p = probability of success on a single trial
- q = probability of failure on a single trial
- n = number of trials
we want to figure out the probability of getting at most 2 heads out of 6 trials , The probability can therefore be found by adding up all the binomial distributions including X=2 and less than it, Thus
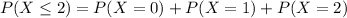
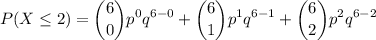
when a coin is tossed, the probability of getting both head (success) and tail (failure) are ½ which is why ,the variables, p and q are assigned to ½. therefore substitute
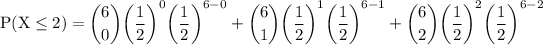
since p and q are the same. it won't make any difference to write all the product of p and q as (½)⁶:
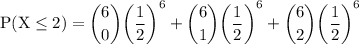
In the expression the term (½)⁶ is common thus factor it out:
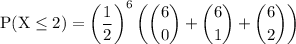
calculate the combinations:
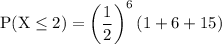
simplify addition:
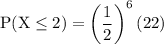
simplify exponent:
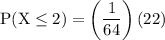
simplify multiplication:
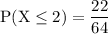
dividing yields:
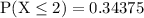
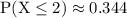
In conclusion
The answer is 0.344