Question

What is the exact maximum and minimum values of f(x)=
`√(x+x^2) -2√(x)` on [0,4]?

Answer 1

`\displaystyle \text{min} = \frac{\sqrt{3+2√(3)}}{2} - \frac{2\sqrt[4]{3}}{√(2)} \text{ at } x = (√(3))/(2)\text{ and } \\ \\ \text{max} = 2√(5) -4 \text{ at } x = 4`

Explanation:

We want to find the maximum and minimum values of the function:

`\displaystyle f(x) = √(x + x^2) - 2√(x)`

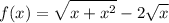
On the interval [0, 4].

First, evaluate its endpoints:

`\displaystyle \begin{aligned} f(0) &= √((0)+(0)^2) - 2√(0) \\ &= 0 \\ \\ f(4) &= √((4)+(4)^2) - 2√((4)) \\ &= 2√(5) -4 \end{aligned}`

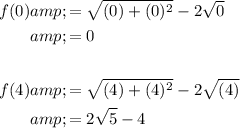
Recall that the extrema of a function occurs at its critical points; that is, where its derivative equals zero (or is undefined).

Take the derivative of both sides:

`\displaystyle f'(x) = (d)/(dx)\left[ √(x + x^2) - 2√(x)\right]`

Differentiate:

`\displaystyle \begin{aligned} f'(x) &= (1)/(2√(x + x^2)) \cdot (1 + 2x) - 2\left((1)/(2√(x))\right) \\ \\ &= (2x+1)/(2√(x+x^2)) - (1)/(√(x)) \\ \\\end{aligned}`

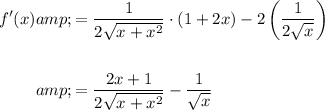
Note that the derivative is undefined at x = 0. Hence, x = 0 is a critical point.

Solve for the zeros of the derivative:

`\displaystyle\begin{aligned} (2x+1)/(2√(x + x^2)) - (1)/(√(x)) &= 0\\ \\ (2x+1)/(2√(x)√(1 + x )) - (1)/(√(x)) &= 0 \\ \\ (2x+1)/(2√(1+x)) - 1 &= 0\\ \\ 2x + 1 &= 2√(1+x) \\ \\ 4x^2 + 4x + 1 &= 4 + 4x \\ \\ x^2 &= (3)/(4) \\ \\ x= (√(3))/(2) \end{aligned}`

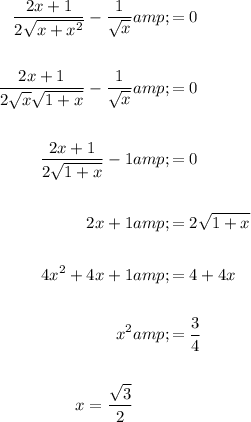
Therefore, our only two critical points are at x = 0 and x = √3/2:

Evaluate the function at x = √3/2:

`\displaystyle \begin{aligned} f\left((√(3))/(2)\right) &= \sqrt{\left((√(3))/(2) \right)+ \left((√(3))/(2)\right)^2} - 2 \sqrt{\left((√(3))/(2)\right)} \\ \\ &= \frac{\sqrt{3+2√(3)}}{2}- \frac{2\sqrt[4]{3}}{√(2)} \\ \\ &\approx -0.5900\end{aligned}`

In conclusion: the exact maximum and minimum values of f on the interval [0, 4] is:

`\displaystyle \text{min} = \frac{\sqrt{3+2√(3)}}{2} - \frac{2\sqrt[4]{3}}{√(2)} \text{ at } x = (√(3))/(2)\text{ and } \\ \\ \text{max} = 2√(5) -4 \text{ at } x = 4`