Answer:
See Below.
Explanation:
We are given the graph of y = f'(x) and we want to determine the characteristics of f(x).
Part A)
f is increasing whenever f' is positive and decreasing whenever f' is negative.
Hence, f is increasing for the interval:
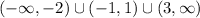
And f is decreasing for the interval:
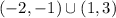
Part B)
f has a relative maximum at x = c if f' turns from positive to negative at c and a relative minimum if f' turns from negative to positive to negative at c.
f' turns from positive to negative at x = -2 and x = 1.
And f' turns from negative to positive at x = -1 and x = 3.
Hence, f has relative maximums at x = -2 and x = 1, and relative minimums at x = -1 and x = 3.
Part C)
f is concave up whenever f'' is positive and concave down whenever f'' is negative.
In other words, f is concave up whenever f' is increasing and concave down whenever f' is decreasing.
Hence, f is concave up for the interval (rounded to the nearest tenths):

And concave down for the interval:
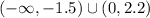
Part D)
Points of inflections are where the concavity changes: that is, f'' changes from either positive to negative or negative to positive.
In other words, f has an inflection point wherever f' has an extremum point.
f' has extrema at (approximately) x = -1.5, 0, and 2.2.
Hence, f has inflection points at x = -1.5, 0, and 2.2.