Question

A gas has a volume of 4.25 m3 at a temperature of 95.0°C and a pressure of 1.05 atm. What temperature will the gas have at a pressure of 1.58 atm and a volume of 2.46 m3

Answer 1

`\boxed {\boxed {\sf 82.7 \textdegree C}}`

Step-by-step explanation:

We are asked to find the temperature of a gas given a change in pressure and volume. We will use the Combined Gas Law, which combines 3 gas laws: Boyle's, Charles's, and Gay-Lussac's.

`\frac {P_1V_1}{T_1}=(P_2V_2)/(T_2)`

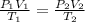
Initially, the gas has a pressure of 1.05 atmospheres, a volume of 4.25 cubic meters, and a temperature of 95.0 degrees Celsius.

`\frac {1.05 \ atm * 4.25 \ m^3}{95.0 \textdegree C}= (P_2V_2)/(T_2)`

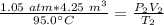
Then, the pressure increases to 1.58 atmospheres and the volume decreases to 2.46 cubic meters.

`\frac {1.05 \ atm * 4.25 \ m^3}{95.0 \textdegree C}= (1.58 \ atm *2.46 \ m^3)/(T_2)`

We are solving for the new temperature, so we must isolate the variable T₂. Cross multiply. Multiply the first numerator by the second denominator, then multiply the first denominator by the second numerator.

`(1.05 \ atm * 4.25 \ m^3) * T_2 = (95.0 \textdegree C)*(1.58 \ atm * 2.46 \ m^3)`

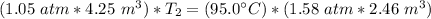
Now the variable is being multiplied by (1.05 atm * 4.25 m³). The inverse operation of multiplication is division, so we divide both sides by this value.

`\frac {(1.05 \ atm * 4.25 \ m^3) * T_2}{(1.05 \ atm * 4.25 \ m^3)} = ((95.0 \textdegree C)*(1.58 \ atm * 2.46 \ m^3))/((1.05 \ atm * 4.25 \ m^3))`

`T_2=((95.0 \textdegree C)*(1.58 \ atm * 2.46 \ m^3))/((1.05 \ atm * 4.25 \ m^3))`

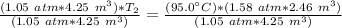
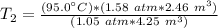
The units of atmospheres and cubic meters cancel.

`T_2=((95.0 \textdegree C)*(1.58* 2.46 ))/((1.05 * 4.25 ))`

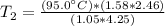
Solve inside the parentheses.

`T_2= ((95.0 \textdegree C)*3.8868)/(4.4625)`

`T_2= (369.246)/(4.4625) \textdegree C}`

`T_2 = 82.74420168 \textdegree C`

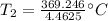
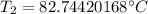
The original values of volume, temperature, and pressure all have 3 significant figures, so our answer must have the same. For the number we calculated, that is the tenths place. The 4 in the hundredth place to the right tells us to leave the 7 in the tenths place.

`T_2 \approx 82.7 \textdegree C`

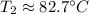
The temperature is approximately 82.7 degrees Celsius.