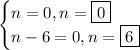Question

Solve by factoring

`{n}^(2) - 6n= 0`
Please show all work!​

Answer 1

`\\ \sf\longmapsto n^2-6n=0`

• Take n common

`\\ \sf\longmapsto n(n-6)=0`

Now

`\\ \sf\longmapsto n=0\:or \:(n-6)=0`

`\\ \sf\longmapsto n=0\:or \;n=6`

Hence roots of the equation are 0 and 6 .

More:-

We can solve it through Quadratic formula

`\boxed{\sf x=(-b\pm √(b^2-4ac))/(2a)}`

Answer 2

`n=0,\\n=6`

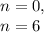
Explanation:

Given
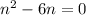`n^2-6n=0`, we can factor out an
`n` from each of the terms on the left side of the equation:

`n(n-6)=0`

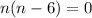
Since we have two factors that multiply to zero, we can set each of them to zero and solve for
`n`, because zero multiplied by anything is equal to zero. Therefore, as long as either
`n` or
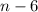`n-6` is equal to zero, the other factor can be any real number and the equation would still hold true.

Therefore, we have the following cases:

`\begin{cases}n=0,\\n-6=0\end{cases}`

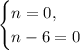
Solving, we get:

`\begin{cases}n=0, n=\boxed{0}\\n-6=0, n=\boxed{6}\end{cases}`