Question

m∠ABC = (9x + 4)° and m∠DEF = (13x − 22)°. If ∠ABC and ∠DEF are supplementary, what is the measure of each angle?

Answer 1

∠ABC measures 85° and ∠DEF measures 95°.

Explanation:

We are given that ∠ABC and ∠DEF are supplementary. Then by definition:

`\displaystyle m\angle ABC + m\angle DE F = 180^\circ`

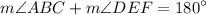
Substitute:

`\displaystyle \left(9x+4\right) + \left(13x-22\right) = 180`

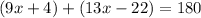
Solve for x. Combine like terms:

`22x -18 = 180`

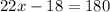
Add:

`\displaystyle 22x = 198`

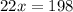
And divide. Hence:

`\displaystyle x = 9`

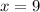
To find the measure of ∠ABC, substitute and evaluate:

`\displaystyle \begin{aligned}m\angle ABC &= 9x + 4 \\ &= 9(9) + 4 \\ &= 81 + 4 \\ &= 85^\circ \end{aligned}`

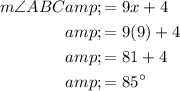
And:

`\displaystyle \begin{aligned}m\\gle DE F &= 13x - 22 \\ &= 13(9) - 22 \\ &= 117-22 \\&= 95^\circ \end{aligned}`

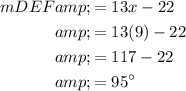
In conclusion, ∠ABC measures 85° and ∠DEF measures 95°.