Answer:

Explanation:
We are given the rational expression:

And we want to find two rational expressions that sum to the above expression.
This technique is known as partial fraction decomposition. First, factor the denominator into linear factors:
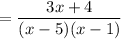
Let A and B be two unknown constants. We can let:
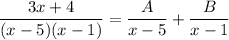
Find A and B. Multiply the entire equation by the denominator:
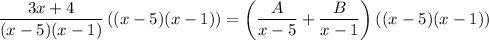
Simplify:
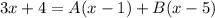
To find A and B, let x equal some value such that it will cancel out one variable. First, let x = 1. Then:
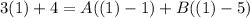
Simplify:

Hence:
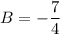
To find A, let x = 5 (we choose this value because it allows us to cancel B):
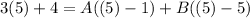
Simplify:
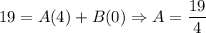
We had:
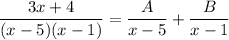
Substitute:
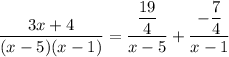
In conclusion:
