Question

Point C is on line segment BD

. Given BD=5x,BC=4x, and CD=4, determine the numerical length of BD.

Answer 1

BD measures 20 units.

Explanation:

We are given that Point C is on the line segment BD, where:

`BD = 5x, BC = 4x \text{ and } CD = 4`

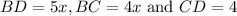
And we want to determine the numerical length of BD.

Since C is somewhere on BD, BD is the sum of BC and CD:

`\displaystyle BD = BC + CD`

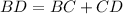
Substitute:

`(5x) = (4x) + (4)`

Solve for x. Subtract:

`x = 4`

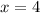
Hence, the value of x is 4.

BD is given by 5x. Therefore:

`BD = 5(4) = 20\text{ units}`

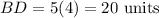
In conclusion, BD measures 20 units.